En esta entrada de blog, veremos cómo construir y entrenar una red neuronal para clasificar imágenes de ropa utilizando el dataset Fashion MNIST con TensorFlow.
A continuación, se explicará en detalle el tipo de red utilizada, su propósito y un desglose de cada parte del código.
¿Qué es el Dataset Fashion MNIST?
Fashion MNIST es un conjunto de datos de imágenes que contiene 70,000 imágenes en escala de grises de 28x28 píxeles, repartidas en 10 categorías.
Es una versión más compleja del clásico dataset MNIST, que contiene dígitos escritos a mano.
Fashion MNIST se utiliza comúnmente para entrenar y evaluar modelos de clasificación de imágenes.
¿Qué Tipo de Red Neuronal Estamos Utilizando y Por Qué?
En este proyecto, utilizamos una Red Neuronal Artificial (ANN) para la tarea de clasificación de imágenes.
¿Por Qué Usar una ANN?
Simplitud y Eficiencia: Las
ANNson relativamente simples de construir y entender, lo que las hace ideales para tareas de clasificación básicas y como introducción al aprendizaje profundo.Tamaño de las Imágenes: Las imágenes de
28x28 píxelesdeldataset Fashion MNISTson lo suficientemente pequeñas para que unaANNpueda manejarlas eficientemente sin requerir la complejidad adicional deredes neuronales convolucionales (CNN), que son más adecuadas para imágenes de mayor resolución.Rapidez en el Entrenamiento: Las
ANNpueden entrenarse rápidamente con datasets de tamaño moderado comoFashion MNIST, permitiendo iteraciones rápidas y ajustes en el modelo.
Estructura de la Red Neuronal Utilizada
Capa de Entrada (Flatten Layer): Convierte cada imagen de
28x28 píxelesen unvector unidimensional de 784 elementos.Capas Ocultas (Dense Layers): Dos capas
densas(fully connected)con 50 neuronas cada una yfunción de activación ReLU. Estas capas capturan patrones y características complejas de las imágenes.Capa de Salida (Dense Layer): Una capa
densacon 10 neuronas yfunción de activación softmax, que produce una probabilidad para cada una de las 10 clases de ropa.
Funciones de Activación
Las funciones de activación son componentes esenciales de las redes neuronales, ya que introducen no linealidad en el modelo, permitiendo que aprenda y represente relaciones complejas. En este modelo, utilizamos las siguientes funciones de activación:
ReLU (Rectified Linear Unit): Es una función de activación muy utilizada en redes neuronales profundas. Se define como
ReLU(x) = max(0, x). La principal ventaja de ReLU es que introduce no linealidad en el modelo y ayuda a mitigar el problema del gradiente desvanecido, permitiendo un entrenamiento más eficiente.Softmax: Esta función de activación se utiliza en la capa de salida de una red neuronal para tareas de
clasificación multiclase. Convierte las salidas de la red en probabilidades, asegurando que la suma de todas las probabilidades sea 1. La clase con la probabilidad más alta es la predicción final del modelo.
Implementación del Código
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
import tensorflow as tf
import tensorflow_datasets as tfds
# Cargar el dataset Fashion MNIST
datos, metadatos = tfds.load('fashion_mnist', as_supervised=True, with_info=True)
# Dividir el dataset en datos de entrenamiento y prueba
datos_entrenamiento, datos_prueba = datos['train'], datos['test']
# Obtener los nombres de las clases
nombres_clases = metadatos.features['label'].names
# Función para normalizar las imágenes
def normalizar(imagenes, etiquetas):
imagenes = tf.cast(imagenes, tf.float32)
imagenes /= 255
return imagenes, etiquetas
# Aplicar la normalización a los datos de entrenamiento y prueba
datos_entrenamiento = datos_entrenamiento.map(normalizar)
datos_prueba = datos_prueba.map(normalizar)
# Cachear los datos para mejorar el rendimiento
datos_entrenamiento = datos_entrenamiento.cache()
datos_prueba = datos_prueba.cache()
# Visualizar una imagen de ejemplo
for imagen, etiqueta in datos_entrenamiento.take(1):
break
imagen = imagen.numpy().reshape((28, 28))
import matplotlib.pyplot as plt
plt.figure()
plt.imshow(imagen, cmap=plt.cm.binary)
plt.colorbar()
plt.grid(False)
plt.show()
# Visualizar las primeras 25 imágenes del dataset de entrenamiento
plt.figure(figsize=(10,10))
for i, (imagen, etiqueta) in enumerate(datos_entrenamiento.take(25)):
imagen = imagen.numpy().reshape((28, 28))
plt.subplot(5,5,i+1)
plt.xticks([])
plt.yticks([])
plt.grid(False)
plt.imshow(imagen, cmap=plt.cm.binary)
plt.xlabel(nombres_clases[etiqueta])
plt.show()
# Construcción del modelo de la red neuronal
modelo = tf.keras.Sequential([
tf.keras.layers.Flatten(input_shape=(28, 28, 1)),
tf.keras.layers.Dense(50, activation=tf.nn.relu),
tf.keras.layers.Dense(50, activation=tf.nn.relu),
tf.keras.layers.Dense(10, activation=tf.nn.softmax)
])
# Compilación del modelo con el optimizador y la función de pérdida
modelo.compile(
optimizer='adam',
loss=tf.keras.losses.SparseCategoricalCrossentropy(),
metrics=['accuracy']
)
# Obtener el número de ejemplos de entrenamiento y prueba
num_ej_entrenamiento = metadatos.splits['train'].num_examples
num_ej_prueba = metadatos.splits['test'].num_examples
TAMANO_LOTE = 32
# Preparar los datos para el entrenamiento
datos_entrenamiento = datos_entrenamiento.repeat().shuffle(num_ej_entrenamiento).batch(TAMANO_LOTE)
datos_prueba = datos_prueba.batch(TAMANO_LOTE)
import math
# Entrenar el modelo
historial = modelo.fit(datos_entrenamiento, epochs=5, steps_per_epoch=math.ceil(num_ej_entrenamiento/TAMANO_LOTE))
# Visualizar la magnitud de la pérdida durante el entrenamiento
plt.xlabel("# Epoca")
plt.ylabel("Magnitud de pérdida")
plt.plot(historial.history["loss"])
plt.show()
import numpy as np
# Realizar predicciones en los datos de prueba
for imagenes_prueba, etiquetas_prueba in datos_prueba.take(1):
imagenes_prueba = imagenes_prueba.numpy()
etiquetas_prueba = etiquetas_prueba.numpy()
predicciones = modelo.predict(imagenes_prueba)
# Función para graficar una imagen con su predicción
def graficar_imagen(i, arr_predicciones, etiquetas_reales, imagenes):
arr_predicciones, etiqueta_real, img = arr_predicciones[i], etiquetas_reales[i], imagenes[i]
plt.grid(False)
plt.xticks([])
plt.yticks([])
plt.imshow(img[...,0], cmap=plt.cm.binary)
etiqueta_prediccion = np.argmax(arr_predicciones)
if etiqueta_prediccion == etiqueta_real:
color = 'blue'
else:
color = 'red'
plt.xlabel("{} {:2.0f}% ({})".format(nombres_clases[etiqueta_prediccion],
100*np.max(arr_predicciones),
nombres_clases[etiqueta_real]),
color=color)
# Función para graficar el valor del arreglo de predicciones
def graficar_valor_arreglo(i, arr_predicciones, etiqueta_real):
arr_predicciones, etiqueta_real = arr_predicciones[i], etiqueta_real[i]
plt.grid(False)
plt.xticks([])
plt.yticks([])
grafica = plt.bar(range(10), arr_predicciones, color="#777777")
plt.ylim([0, 1])
etiqueta_prediccion = np.argmax(arr_predicciones)
grafica[etiqueta_prediccion].set_color('red')
grafica[etiqueta_real].set_color('blue')
# Visualizar las predicciones
filas = 5
columnas = 5
num_imagenes = filas*columnas
plt.figure(figsize=(2*2*columnas, 2*filas))
for i in range(num_imagenes):
plt.subplot(filas, 2*columnas, 2*i+1)
graficar_imagen(i, predicciones, etiquetas_prueba, imagenes_prueba)
plt.subplot(filas, 2*columnas, 2*i+2)
graficar_valor_arreglo(i, predicciones, etiquetas_prueba)
plt.show()
# Realizar una predicción individual
imagen = imagenes_prueba[10]
imagen = np.array([imagen])
prediccion = modelo.predict(imagen)
print(f"Prediccion: {nombres_clases[np.argmax(prediccion[0])]}")
Explicación Detallada del Código
Importar Bibliotecas Necesarias
1
2
import tensorflow as tf
import tensorflow_datasets as tfds
Aquí, importamos TensorFlow para construir y entrenar nuestra red neuronal y TensorFlow_Datasets para cargar el dataset Fashion MNIST.
Cargar y Dividir el Dataset
1
2
3
datos, metadatos = tfds.load('fashion_mnist', as_supervised=True, with_info=True)
datos_entrenamiento, datos_prueba = datos['train'], datos['test']
nombres_clases = metadatos.features['label'].names
Cargamos el dataset Fashion MNIST y lo dividimos en datos de entrenamiento y prueba. También obtenemos los nombres de las clases para etiquetar las imágenes.
Normalizar las imágenes
1
2
3
4
5
6
7
8
9
def normalizar(imagenes, etiquetas):
imagenes = tf.cast(imagenes, tf.float32)
imagenes /= 255
return imagenes, etiquetas
datos_entrenamiento = datos_entrenamiento.map(normalizar)
datos_prueba = datos_prueba.map(normalizar)
datos_entrenamiento = datos_entrenamiento.cache()
datos_prueba = datos_prueba.cache()
Definimos una función para normalizar las imágenes (escalar los valores de los píxeles entre 0 y 1) y aplicamos esta función a los datos de entrenamiento y prueba.
También cacheamos los datos para mejorar el rendimiento.
Visualizar Imágenes de Ejemplo
1
2
3
4
5
6
7
8
9
10
11
for imagen, etiqueta in datos_entrenamiento.take(1):
break
imagen = imagen.numpy().reshape((28, 28))
import matplotlib.pyplot as plt
plt.figure()
plt.imshow(imagen, cmap=plt.cm.binary)
plt.colorbar()
plt.grid(False)
plt.show()
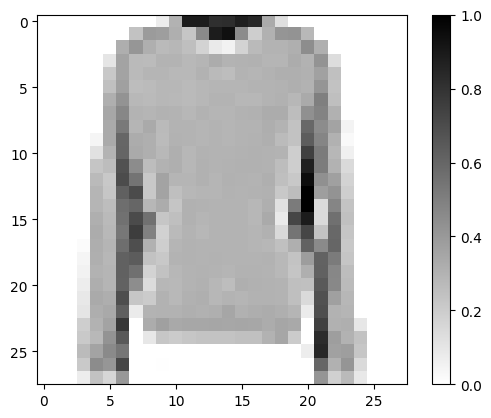
Visualizamos una imagen de ejemplo del dataset de entrenamiento para entender mejor los datos con los que estamos trabajando.
Salida:
Visualizar las Primeras 25 Imágenes del Dataset de Entrenamiento
1
2
3
4
5
6
7
8
9
10
plt.figure(figsize=(10,10))
for i, (imagen, etiqueta) in enumerate(datos_entrenamiento.take(25)):
imagen = imagen.numpy().reshape((28, 28))
plt.subplot(5,5,i+1)
plt.xticks([])
plt.yticks([])
plt.grid(False)
plt.imshow(imagen, cmap=plt.cm.binary)
plt.xlabel(nombres_clases[etiqueta])
plt.show()
Mostramos las primeras 25 imágenes del dataset de entrenamiento con sus etiquetas correspondientes.
Salida:
Construcción del Modelo de la Red Neuronal
1
2
3
4
5
6
modelo = tf.keras.Sequential([
tf.keras.layers.Flatten(input_shape=(28, 28, 1)),
tf.keras.layers.Dense(50, activation=tf.nn.relu),
tf.keras.layers.Dense(50, activation=tf.nn.relu),
tf.keras.layers.Dense(10, activation=tf.nn.softmax)
])
Definimos un modelo secuencial con una capa de aplanamiento (flatten), dos capas densas con 50 neuronas cada una y función de activación ReLU, y una capa de salida con 10 neuronas y función de activación softmax.
Compilación del Modelo
1
2
3
4
5
modelo.compile(
optimizer='adam',
loss=tf.keras.losses.SparseCategoricalCrossentropy(),
metrics=['accuracy']
)
Compilamos el modelo especificando el optimizador Adam, la función de perdida de entropía cruzada categórica escasa y la métrica de precisión.
Preparación de los Datos para el Entrenamiento
1
2
3
4
5
6
7
num_ej_entrenamiento = metadatos.splits['train'].num_examples
num_ej_prueba = metadatos.splits['test'].num_examples
TAMANO_LOTE = 32
datos_entrenamiento = datos_entrenamiento.repeat().shuffle(num_ej_entrenamiento).batch(TAMANO_LOTE)
datos_prueba = datos_prueba.batch(TAMANO_LOTE)
Obtenemos el número de ejemplos de entrenamiento y prueba.
Configuramos el tamaño del lote y preparamos los datos para el entrenamiento, repitiéndolos, barajándolos y dividiéndolos en lotes.
Entrenamiento del Modelo
1
2
3
import math
historial = modelo.fit(datos_entrenamiento, epochs=5, steps_per_epoch=math.ceil(num_ej_entrenamiento/TAMANO_LOTE))
Entrenamos el modelo durante 5 épocas (vueltas), calculando el número de pasos por época.
Visualización del Proceso de Entrenamiento
1
2
3
4
plt.xlabel("# Epoca")
plt.ylabel("Magnitud de pérdida")
plt.plot(historial.history["loss"])
plt.show()
Graficamos la magnitud de la pérdida durante las épocas de entrenamiento para entender cómo el modelo mejora con el tiempo.
Realización de Predicciones
1
2
3
4
5
6
import numpy as np
for imagenes_prueba, etiquetas_prueba in datos_prueba.take(1):
imagenes_prueba = imagenes_prueba.numpy()
etiquetas_prueba = etiquetas_prueba.numpy()
predicciones = modelo.predict(imagenes_prueba)
Realizamos predicciones en un lote de datos de prueba y almacenamos las predicciones junto con las imágenes y etiquetas reales.
Visualización de Predicciones
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
def graficar_imagen(i, arr_predicciones, etiquetas_reales, imagenes):
arr_predicciones, etiqueta_real, img = arr_predicciones[i], etiquetas_reales[i], imagenes[i]
plt.grid(False)
plt.xticks([])
plt.yticks([])
plt.imshow(img[...,0], cmap=plt.cm.binary)
etiqueta_prediccion = np.argmax(arr_predicciones)
if etiqueta_prediccion == etiqueta_real:
color = 'blue'
else:
color = 'red'
plt.xlabel("{} {:2.0f}% ({})".format(nombres_clases[etiqueta_prediccion],
100*np.max(arr_predicciones),
nombres_clases[etiqueta_real]),
color=color)
def graficar_valor_arreglo(i, arr_predicciones, etiqueta_real):
arr_predicciones, etiqueta_real = arr_predicciones[i], etiqueta_real[i]
plt.grid(False)
plt.xticks([])
plt.yticks([])
grafica = plt.bar(range(10), arr_predicciones, color="#777777")
plt.ylim([0, 1])
etiqueta_prediccion = np.argmax(arr_predicciones)
grafica[etiqueta_prediccion].set_color('red')
grafica[etiqueta_real].set_color('blue')
filas = 5
columnas = 5
num_imagenes = filas*columnas
plt.figure(figsize=(2*2*columnas, 2*filas))
for i in range(num_imagenes):
plt.subplot(filas, 2*columnas, 2*i+1)
graficar_imagen(i, predicciones, etiquetas_prueba, imagenes_prueba)
plt.subplot(filas, 2*columnas, 2*i+2)
graficar_valor_arreglo(i, predicciones, etiquetas_prueba)
plt.show()
Definimos funciones para graficar las imágenes junto con las predicciones y los valores de predicción.
Luego, visualizamos las predicciones para un conjunto de imágenes de prueba.
Realización de una Predicción Individual
1
2
3
4
5
imagen = imagenes_prueba[10]
imagen = np.array([imagen])
prediccion = modelo.predict(imagen)
print(f"Prediccion: {nombres_clases[np.argmax(prediccion[0])]}")
Seleccionamos una imagen de prueba y realizamos una predicción individual para ver el resultado.
Conclusión
Este ejercicio demuestra cómo construir y entrenar una red neuronal para la clasificación de imágenes de ropa utilizando el dataset Fashion MNIST. Hemos explorado desde la carga y preprocesamiento de datos hasta la visualización de predicciones, proporcionando una visión completa del flujo de trabajo en el aprendizaje profundo con TensorFlow.
Espero que os haya gustado y servido, cualquier comentario es de mucha ayuda. Adios!